Reader Mike V castigates me for over-use of logs.

I’m not at all averse to logs, but they have a time and a place. You are trying to point out relatively small changes in income over a short time-series – not the nearly exponential changes in the S&P 500 over the last 100+ years.

Let me provide some examples of where it’s useful to use logs [logarithms]. First, consider the dollar’s value over the course of a year and a half (somewhat less than 100+ years).

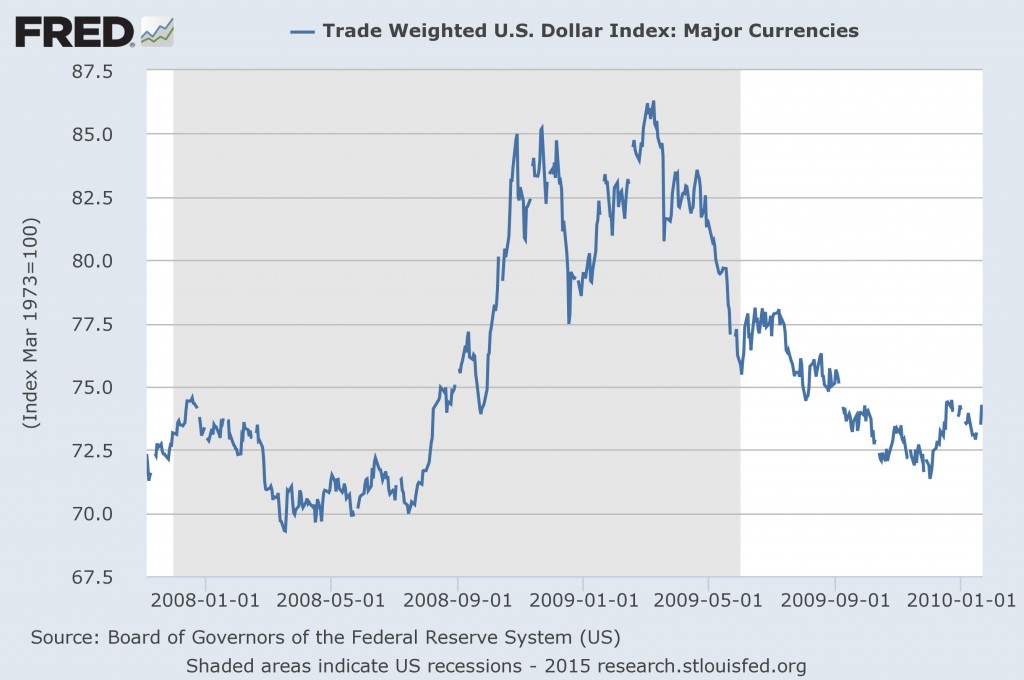
Source: Federal Reserve Board via FRED.

Now let’s consider trough to peak, and peak to trough, changes. From July 15, 2008 to March 9, 2009, the dollar appreciated 23.34%, using the formula (Q2-Q1)/Q1. From March 9 to December 2, 2009, the dollar depreciated 17.10%, using (Q3-Q2)/Q2. Dollar up by 23.34%, down by 17.10% — one might think the dollar was up overall by 6.24%. But in fact, using the base period formula (Q3-Q1)/Q1, the dollar is up by 2.24%.

One advantage of using changes in log terms is that additivity is retained, as Jim mentioned in an earlier post; using a log approximation of log(Q2/Q1), one finds the appreciation is 20.98%, the depreciation is 18.76%, the net change is 2.22%. And this is exactly what one gets looking directly at the log change from July 15, 2008 to December 2, 2009.

Second, a more recent, and stark, example is the Chinese stock market (discussed here and by Jeff Frankel). From July 11, 2014 to June 12, 2015, the Shanghai and Shenzhen CSI 300 index rises by 148.33% (using the base period formula), and then falls 28.21% by August 3 (2148 to 5334 to 3829). The August 3 value is 78.27% above the July 11, 2014 value (and not 120.12% that a simple adding and subtracting would have given you). And this all happens in the space of 13 months…

Third, for those of us who work in international finance, there is yet another reason we use logs. Consider the dollar/euro exchange rate; there are two equally valid ways of quoting the rate — the number of dollars per euro, and the number of euros per dollar. If one express S as USD/EUR, and calculated the annual percent change using the base period formula, one would find that one would not get the negative of the annual percent change of 1/S in units of EUR/USD. (One would, if the depreciation rates were calculated using log differences.) To make this more concrete, from the US perspective, dollar has appreciated 19.1% from June 2014 to July 2015, while from the Euro area perspective the euro has depreciated by 23.6%.

See also Jim’s post on the use of logs.

The next post on logs will address whether to estimate a cointegrating relationship in levels of consumption and disposable income, or whether it is more advisable to do so in log-levels.

>> Read Part II: To Log Or Not To Log