The chart displayed near the end of this discussion is effectively a pictorial representation of what Keynesian economists call a paradox* (“Gibson’s Paradox”) and Austrian economists call a natural and perfectly understandable relationship.

Gibson’s Paradox was the name given by JM Keynes to the observation that interest rates during the gold standard were highly correlated to wholesale prices but had little correlation to the rate of “inflation”, that is, that interest rate movements were connected to the level of prices and not the rate of change in prices. It was viewed as a paradox because most economists couldn’t explain it. According to conventional wisdom, interest rates should have been positively correlated with the rate of “price inflation”.

The problem is that most economists did not — and still do not — understand what interest rates are.

First and foremost, interest rates are the price of time. They reflect the fact that, all else being equal, humans place a higher value on getting something now than on getting exactly the same thing at some future time. Interest rates transcend money, because they exist even when money does not. With or without money and all else being equal, getting something now will always be worth more than getting the same thing in the future**. This is called time preference.

Time preference is the root of interest rates and the natural interest rate is a measure of societal time preference. That is, the natural interest rate is a measure of the general urgency to consume in the present or the amount that would have to be paid, on average, to make saving (the postponement of consumption) worthwhile. For example, the average 7-year-old child has a very high time preference, in that if you give the kid a choice between getting a desirable toy today or getting something more in 3 months’ time, the “something more” option won’t be chosen unless it is a LOT more, whereas a middle-aged adult with substantial savings is likely to have low time preference.

When interest rates are properly understood it becomes clear that the paradox named after Gibson is no paradox at all. The reason is that if the money is sound, as it mostly was under the Gold Standard, both interest rates and prices will move in the same direction in response to changes in societal time preference.

To further explain, during a period of rising time preference, that is, during a period when there is an increasing desire to consume in the present, the prices of goods will rise (on average) due to increasing demand and it will take a higher interest rate to encourage people to delay their spending. During a period of falling time preference, that is, during a period when there is an increasing desire to save, the prices of goods will fall (on average) and people will generally accept a lesser incentive (interest rate) to delay their spending.

In a nutshell, there is no paradox because, when the money is sound, interest rates don’t drive prices and prices don’t drive interest rates; instead, on an economy-wide basis*** both prices and interest rates are driven by changes in societal time preference.

That’s all well and good, but we no longer have sound money. Moreover, we have massive, continuous manipulation of interest rates by central banks. The signal that interest rates should send is therefore now being overwhelmed by central-bank-generated noise to the point where it’s a miracle (a testament to the resilience of entrepreneurial spirit, actually) that we still have a functioning economy. Quite remarkably, though, signs of the age-old relationship between interest rates and the price level can still be found if you know where to look.

The signs aren’t apparent when interest rates are compared with an official wholesale price index, because a great effort is expended by the central planners to ensure that the official money loses purchasing power year-in and year-out regardless of what’s happening in the world. However, the signs are apparent when interest rates are compared to a wholesale price index based on gold.

The commodity/gold ratio is the price of a broad-based basket of commodities in gold terms. In essence, it is a wholesale price index using gold as the monetary measuring stick. Although gold is no longer money in the true meaning of the term (it is no longer the general medium of exchange), it is still primarily held for what can broadly be called ‘monetary purposes’ and in many respects it trades as if it were still money. According to the age-old relationship discussed above and labeled “Gibson’s Paradox” by a confused JM Keynes, the commodity/gold ratio should generally move in the same direction as risk-free interest rates.

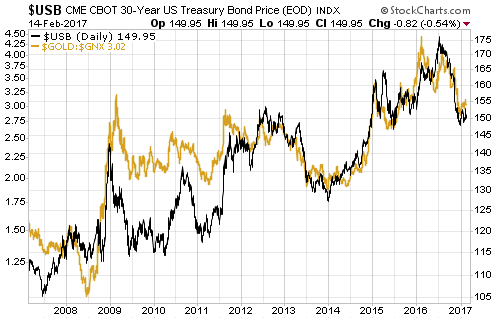
The risk-free US interest rate that is least affected by the direct manipulation of the Fed is the yield on the 30-year T-Bond, so what we should see is a positive correlation between the commodity/gold ratio and the T-Bond yield. Or, looking at it from a different angle, what we should see is a positive correlation between the gold/commodity ratio and the T-Bond price. That’s exactly what we do see.

Using the Goldman Sachs Spot Commodity Index (GNX) to represent commodities, the following chart shows that the age-old relationship has worked over the past 10 years when gold is the monetary measuring stick. It has also worked over the past 20 years, although there was a big divergence — possibly due to the ‘China effect’ on commodity prices or the ECB’s aggressive money pumping — in 2005.

I like this chart because it makes economic sense and because it can be helpful when trying to anticipate the next important turning point for the gold/commodity ratio and/or the T-Bond.

*As a general rule, if your theory leads to a paradox then your theory is wrong.

**There are many real-life examples of a premium being paid to receive a good in the future rather than the present, but in such cases all is not equal. That is, in such cases there will be a difference between the future good and the present good that makes the future good more valuable. For example, an oil refiner will generally pay more for a barrel of oil to be delivered in six months’ time than a barrel of oil to be delivered immediately, because if it doesn’t plan to refine the oil until 6 months from now it can save 6 months of storage costs by purchasing oil for future delivery. To put it another way, in this oil-refiner example a barrel of oil for immediate delivery is priced at a discount because it comes with 6 months of storage-related baggage.

***For any specific interest-rate-related transaction, credit risk will be very important. As a result, at any given time there will be a wide range of interest rates within an economy even if the money has no “inflation” risk. However, it is reasonable to think of time preference as an interest-rate floor that rises and falls. In effect, time preference determines the interest rate that would apply on average throughout the economy if there were no credit or inflation risks.