Nonlinear Models Give No Escape From R*
The dynamic stochastic general equilibrium (DSGE) model literature is ever-growing, and new features are being continuously added. This makes it difficult to make generalizations about the literature. However, from a macro modelling perspective, we are mainly interested in models that might be used by a central bank to set interest rates. Even if we are not central bankers ourselves, we presumably want to understand how central bankers see their policy lever as working.
In an earlier article (link), I discussed how all linear models end up with a notion that there is a "neutral" interest rate at any given time -- a policy rate which does not lead the economy to accelerate in one direction or another. If we add standard assumptions made by neoclassical economists, we can get to the concept of r* -- which is a steady state neutral rate. (If we are away from that steady state, the neutral rate within a linear model at any given time is determined by the deviations of other values from their steady states.)
The implication is that if we take a linearisation of any DSGE model that meets standard rules for acceptability for neoclassical economists, we end up with a model that has an embedded r*. This means that most of our analytical effort in the real world is coming up with a good estimate of r* (and the steady state levels other variables that are supposed to be driving the economy). There is a not immediately obvious implication: if r* estimates behave in a pathological fashion, we have reasons to question any of those linearisations. Since my argument is that this is exactly what is happening, this would be worrisome for DSGE model fanciers.
The question then arises: can a transition to a nonlinear model reduce the dependence upon r*? My argument is that this is not the case, at least for models that we can hope to fit to observed data.
Interest Rate Neutrality at a Point in Time
The premise for my discussion is straightforward: imagine you are a central banker, who insists that an inflation target is to be hit. We will assume that the economy is is some form of non-pathological steady state, and so interest rate policy works as is conventionally expected.
We assume that we are conventional economists, and assume that the real policy rate (r(t)) matters, and that the inflation rate does not do pathological things that cancels out movements in the nominal interest rate. As such, at a fixed time point t, we can set the real interest rate r(t).
I discussed various technical issues with this viewpoint in the previous article. One angle that pedantic people might latch onto is the story that central banks have reaction functions within DSGE models, and do not set the interest rate one period at a time. However, as a I noted in the linked article on linear models, we can add a constant to any reaction function to get control over the current period's interest rate.
I am ignoring the issue of the zero lower bound; whether or not a particular real rate is achievable is not the concern, rather the effect on the model output when the real rate is achieved.
Finally, I used the notion of acceleration in the previous article. Since I want to capture as many models as possible with my description, I do not specify exactly how interest rates effect the economy. All that matters is that the interest rate influences the economy in such a fashion so as to allow an inflation target (or other target) to be hit. I label this acceleration since it is often thought of as an acceleration in GDP, but this should not be taken literally. We just need something that offers a numerical summary of the effect of a policy rate change on the economy. I would also note that the acceleration may follow the policy rate with a lag, and may be some form of an average of the response to a step change in the policy rate.
Why Conventional Assumptions?
In my discussion, I refer to the effects of interest rates following conventional assumptions. Since published DSGE models that are taken seriously be central bankers follow these assumptions, this is not restrictive when discussing those models. (Of course, they would be restrictive if we started looking at heterodox models.)
There are a number of reasons why one would confine attention to conventional models. From a mainstream perspective, the argument is that is how reality works. However, one could attach more cynical reasons behind this, such as the likelihood of losing research funding from central banks if one gets too wacky with the models.
Can Nonlinear Models Escape r*?
With the preliminaries out of the way, we can turn to the question of whether nonlinear models can escape the theoretical gravity or r*? Although we can imagine a variable meeting the formal definition of r* not existing, it is nearly impossible to get away from a one-period "neutral" rate.
Our first observation is that we need to rule out many possible classes of nonlinear models. The problem with nonlinear mathematical systems is that they are extremely general, and it is nearly impossible to say anything useful about them. However, we need some nice properties, as otherwise we could never fit them to data.
Our first step is to rule out models that are not continuous with respect to the policy rate at time t (r(t)). For example, some joker might write down a model where the behaviour is different whether the real policy rate is rational or not. We need to have the function to be relatively well-behaved over the range of values that are encountered in past history. (E.g., we do not really care about pathological behaviour if interest rates go to infinity.)
The rest of this article will run through potential shapes of such functions, and see why we can reject most -- if we assume that interest rate policy acts in a conventional fashion.
No Way to Control the Economy -- Nope
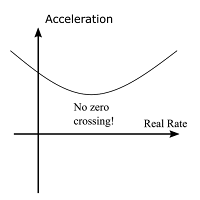
The first possible functional shape is one where the acceleration as a function of the real rate is always one sign. This implies that there is no way for interest rate policy to influence the economy -- it is always accelerating or decelerating.
This runs afoul of the conventional thinking assumption, which assumes that it is possible to control the economy with interest rates.
Please note that I am assuming that the model is operating under normal conditions. It is perfectly acceptable that interest rate policy is ineffective for a short period of time; e.g., during a financial crisis that impairs the banking system.
Wrong Sign -- Nope
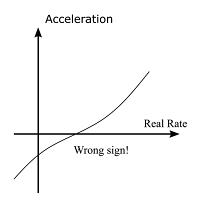
The next possibility is that interest rate policy has the wrong sign relative to conventional thinking. That is, higher real rates cause the economy to accelerate.
On paper, such a configuration would be acceptable, and does not effect my discussion. However, it would be ruled out by assumption i practice.
Expected Model -- Can Be Linearised

The version of the function that is acceptable is one that has a single crossing of the zero point, and has the desired monotonic decline in acceleration as a function of the real policy rate.
It should be noted that this clean behaviour need only show up over ranges of interest rates that are typically observed in the real world. We do not care too much about theoretical oscillations that happen if the real rate hits 100%.
We can appeal to the Taylor expansion to show that there should be a linear approximation of the nonlinear function that holds near the zero crossing (single period neutral rate). Technically, we might need to appeal to some wider notion of a derivative (generalised derivatives) if the function is continuous but not differentiable. (For example, the slope of the approximation might be different on either side of the zero crossing.)
This is the story that central bankers want to hear: if they set the real policy rate above this level, the economy decelerates, and accelerates if it is below that level. We just need to be able to figure out how that neutral point evolves over time.
Other Cases Too Complex
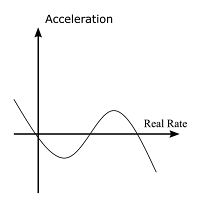
We can then think about more complex cases, and realise that the implied models are unlikely to be fit to data.
Take the example to the left, where there are three zero crossings. The first zero crossing (near the acceleration axis marking) looks like the conventional story. The problem is the transition to the second crossing. We get another neutral rate, but the reaction around this point is backwards -- increases causes acceleration. The function then whips around, and then acts conventionally around the third zero crossing.
Although we could come up with stories that generate such a reaction (differing sectors having different reactions to interest rates, interest payments on government debt providing stimulus), such a function is going to be a nightmare to fit to data. Not only is it hard to discern the effect of interest rates on the acceleration variable (since it will be affected by other variables that we are ignoring), we now have to estimate where the various zero crossings are (since I am assuming that the range of the graph corresponds to the range of observed real rates).
We are facing a problem that is more of philosophy than economics. We could imagine that a model that generates a response curve that looks like this is the "best" model of the economy. But if it is impossible to fit the model to observed data, in what sense is it the best model?
Economies are not like engineering systems where we can subject them to varying inputs under controlled conditions to see the response. Policymakers react in a fairly predictable fashion to economic data, and so we have a very limited data set. I have severe doubts that a model with a response like this would ever be fit to data.
Threshold Issues
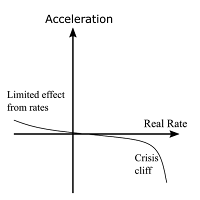
My bias is that the real world reaction function is qualitatively similar to what we see in this figure. The response to interest rates is relatively small over most of the observed data set. However, if the real rate is cranked up to a high enough level, it is enough to induce a financial crisis, and thus a recession. This response function could easily explain most observed data. In particular, it suggests that central bankers are normally pushing on a string -- until they manage to blow up the economy.
Although this picture is not far from conventional views, it will be shunned, as it implies that monetary policy is ineffective for fine-tuning the economy to allow for optimal outcomes. Since many economists want to role-play as 1960s optimal control engineers, this is the wrong answer.
Attempting to fit such a response to data will be tough. It is seems quite likely that the cliff level will vary with time, depending on the state of balance sheets of the private sector. Meanwhile, central bankers have not induced enough financial crises to offer much of a data set to work with. New Keynesian central bankers are extremely timid versus their early-1980s crypto-Monetarist counterparts, and the private sector has tended to blow up on its own. That is, central bankers did not probe for the threshold level with high enough rates, and then the economy tanked once the financial system blew up.
Nonlinear Models: Worthwhile or Not?
If one looks at linearised DSGE models, the typical response is that one is way behind the times. This is certainly true if we want to look at teaching models (link to discussion of teaching versus empirical models). However, teaching models are used to spin yarns about the economy. They have their uses, but sooner or later, we need to go beyond spinning yarns. We need to fit the model to data. The ugly reality is that the assumed structure of DSGE models means that the nonlinear model fitting cannot diverge too drastically from that of linear models.
I will note that I have not done a survey of the DSGE literature in some time. However, I doubt that the situation will have radically changed. Most papers discussing nonlinear models attempt to throw every bit of dazzling mathematics possible at the reader, but refuse to deal with rudimentary "so what?" questions in plain English. The empirical work is designed to impress other neoclassical economists, but not answer reasonable questions about the quality of the model fit to reality.
As such, I expect that we are still stuck with the need to estimate r* and its theoretical cousins, since tractable models will end up have responses that are close to linear.
Disclaimer: This article contains general discussions of economic and financial market trends for a general audience. These are not investment recommendations tailored to the particular needs of an ...
more


