Growth Rate Of The GDP Per Capita Revisited. The Results From 2007, 2009, And 2012 Revisited
Growth rate of the GDP per capita revisited. 3. The results from 2007, 2009, and 2012 revisited. The model
GDP per capita data revisited
We start with a revision of the period after 1950. Originally, we estimated the evolution of annual increment before 2003. Then data for the period between 2004 and 2007 were added the prediction of the model was estimated. In 2012, 4 new readings were added for all involved countries. In 2006, we made a model-based assumption (see Appendix in this post for the model description) that all large deviations from the linear trend in the annual GDP per capita should fade away in the near future. In this post, we claim that this assumption was an extremely successful one and it statistically validates the model of linear GDP per capita growth.
The upper panel of Figure 1 is borrowed from the 2012 paper and presents the comparison of GDP per capita in Austria for the period between 1950 and 2011. The positive slope reported in 2008 (black line, slope=0.012 $/$) decreased between 2007 and 2011 (red line, slope=0.0064 $/$), as predicted. Since 2007, the period of low economic performance with an extended recession resulted in a further decline in the speed of economic growth and the lower panel of Figure 1 shows that the slope (the MPD data are used for this analysis) fell to 0.0014 $/$. In 2018, the linear regression (black) line is not much different from the mean value (red dotted) line. Figure 2 presents a similar analysis made for the USA where the slope for the period between 1951 and 2018 is close to that observed for the period between 1950 and 2011 because the major fall in economic growth was between 2008 and 2010. The mean value between 1951 and 2018 is $569, i.e. slightly higher than that in Austria.
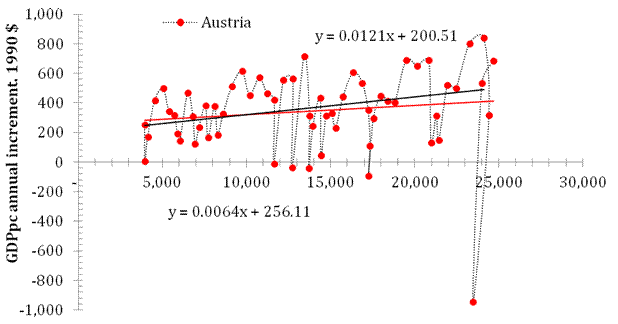
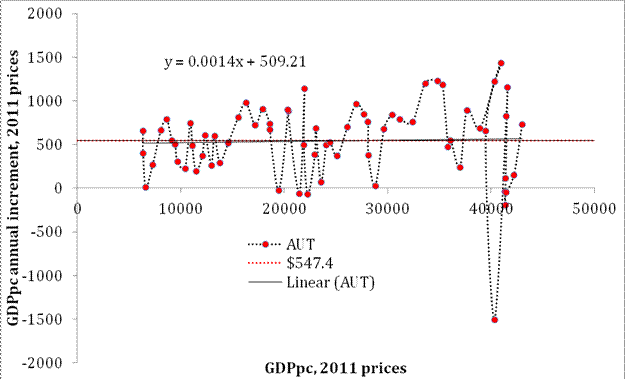
Figure 1. The upper panel: annual increment of real GDP per capita (in 1990 US dollars) as a function of real GDP per capita in Austria for the period between 1951 and 2011. The regression (red) line slope is $0.0064 per dollar. For the period between 1951 and 2007, the regression (black) line has a larger slope of $0.012 per dollar. The lower panel: Same as in the upper panel for the period between 1951 and 2018. The slope fell to $0.014 per $ (2011 prices). The mean GDPpc annual increment value is $547.4.


Figure 2. Same as in Figure 1 for the USA. The slope for the period between 1951 and 2018 is close to that observed for the period between 1950 and 2011 because the major fall in economic growth was between 2008 and 2010. The mean value between 1951 and 2018 is $569, i.e. slightly higher than that in Austria.
In the future post, we will revisit other countries and present the evolution of annual GDPpc increment between 1960 and 2018. The change is the studied period is justified in the previous post. Our principal aim is to prove that the model we have developed accurately predicts the economic growth in developed countries. Moreover, it gives an unbiased and theoretically justified view on the current rate of relative growth in GDPpc in various countries depending on the GDPpc level. One should not compare the relative rate of economic growth in China (GDPpc is $13102 in 2018) and in the USA (GDPpc=$55335 in 2018). One should compare the annual increments in the GDPpc and corresponding rates predicted by the model for inertial economic growth. In that sense, the USA growth rate is much higher than that observed in China. However, the population in China is 4 times larger than in the USA and this gives an impression of faster economic growth in the former.
Appendix. The model
Let me repeat the major features of our concept describing the evolution of real Gross Domestic Product (GDP). The principal claim is simple – the growth rate, g(t), of real GDP per capita, G(t), is driven by the attained level of real GDP per capita and the change in a country dependent on a specific age population, Ns. The growth rate of the real GDP per capita in developed countries is characterized by a constant annual increment, A. All fluctuations around this constant increment can be explained by the change in the number of people of the country-specific age:
g(t) = dlnG(t)/dt = A/G(t) + 0.5dlnNs(t)/dt (1)
Equation (1) is a quantitative model that has been constructed empirically and proved statistically by cointegration tests.
In economic statistics, usually, the relative growth rate is published, as represented by dG(t)/G(t)=dlnG(t). For the sake of simplicity, we assume that the second term in (1) is zero. Accordingly, the economic system under study is in a stationary or inertial growth, i.e. A/G(t) is “the inertial growth” as in physics. The adults between 15 and 64, i.e. in the working-age population, can be also considered as living in a stationary regime since no dramatic organic and functional changes happen to their life process out of the margins of natural variations.
For the inertial growth, the real GDP per capita grows as a linear function of time:
g(t) = dlnG(t)/dt(given dNs(t) = 0) = A/G(t)
G(t) = At + C (2)
where G (t) is completely equivalent to the inertial growth, Gi(t), i.e. the first component of the overall growth as defined by (1). Relationship (2) defines the linear trajectory of the GDP per capita, where C=Gi(t0)=G(t0) and t0 is the starting time. In the regime of inertial growth, the real GDP per capita increases by the constant value A per time unit. Relationship (3) is equivalent to (2), but holds for the inertial part of the total growth:
Gi(t) = Gi(t0) + At (3)
The relative rate of growth along the inertial linear growth trend, gi(t), is the reciprocal function of Gi or, equivalently, G:
gi(t) = dlnGi/dt = A/Gi = A/G(t) (4)
Relationship (4) implies that the rate of GDP growth will be asymptotically approaching zero, but the annual increment A will be constant. Moreover, the absolute rate of the GDP per capita growth is constant and is equal to A [$/y]. This constant annual increment thus defines the constant “speed” of economic growth in a one-to-one analogy with Newton’s first law. Hence, one can consider the property of constant speed of real economic growth as “inertia of economic growth” or simply “inertia”. Then the growth, which is observed without the change in the specific age population, can be called the “inertial growth”.
In physics, inertia is the most fundamental property. In economics, it should also be a fundamental property, taking into account the difference between the ideal theoretical equilibrium of space/time and the stationary real behavior of the society. Mechanical inertia implies that no change in motion occurs in the absence of net external force and without a change in internal energy. (In the real world, the net force is zero for constant speed, but one should apply extra forces in order to overcome the net traction force and to keep the body (e.g., car) moving at a constant speed.) For a society, the net force applied by all economic agents is not zero but counteracts all dissipation processes and creates goods and services in excess of the previous level. The economy does grow with time and its “internal energy” as expressed in monetary units does increase at a constant speed.
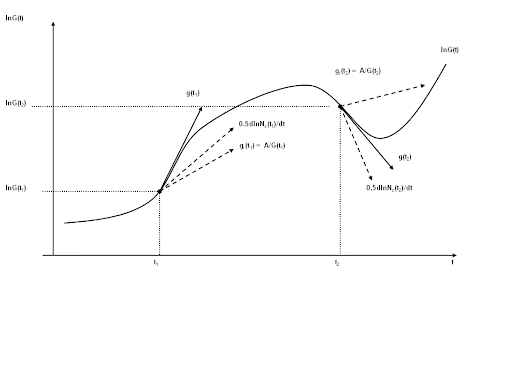
Figure 3. Illustration of the growth model for real GDP per capita
Figure 3 depicts an arbitrary GDP evolution curve, lnG(t), which shows episodes of rapid growth (t1) and recession (t2). It is easier to illustrate the performance of the model on extreme cases and then to proceed by showing how GDP growth relates to the two defining components at t1 and t2.
The growth rate is nothing but the first derivative of the function lnG(t). So, we are interested in how the tangent of the curve behaves. Let’s first consider the case of the rapid growth in t1. The overall growth rate g(t1) is the tangent to the curve at point t1. Please notice that if the age-specific population is fixed (dNs(t1) = 0), the inertial growth rate gi would be the tangent to the lnG(t). Nevertheless, we observe that dlnNs(t) > 0 what results in a rise in the GDP above the inertial level of growth.
The second case is similar but differs in the direction of the overall growth. Please notice that gi(t1) > gi(t2) as the attained level of real GDP per capita is higher at t2 and A/G(t1)>A/G(t2). Furthermore, the rate of change of the age-specific population is negative, which leads to the overall negative growth as the GDP declines
Disclosure: None.