The core of any fixed income pricing model is a yield or discount curve. The discount curve allows for arbitrage-free pricing of all instruments without optionality -- which I refer to here as linear instruments (which may be a slight bending of terminology). Instruments with optionality are nonlinear instruments, which add considerable complexity to fixed income option pricing. This article discusses the properties of the part of the model that prices the linear instruments. Since the linear pricing is only dependent upon the expected value of the probability distribution -- and not the shape of the distribution -- it is unaffected by option pricing, and so it can be fitted before attempting to price options.

This article assumes that the reader is familiar with the concept of arbitrage (link to primer) as well as the basic of yield curves (link to primer). A small amount of material will be reviewed to keep this article self-contained. I will not address the mathematics, instead the objective here is to explain what the mathematics means.

Linear Instruments: Swaps, Bonds, Futures, and Forwards

We are interested in pricing linear instruments that are assumed to be free of default risk. The underlying instruments are either bonds or bills issued by floating currency sovereigns, or swaps. (Although a bank can go bankrupt, the floating rate reference -- historically LIBOR -- cannot.)  We can add in stripped bonds (zero coupon bonds) some derivative instruments, either forwards or futures, (plus whatever we classify repo trades as).

In the real world, there are many technical effects that can affect pricing, e.g., the bias between short-term interest rate futures and swaps. We adjust our pricing from the theoretical fair value to compensate.

Instruments that are excluded include callable bonds, swaptions, caps and floors, futures options. Instruments with default risk would mess everything up as well. We need much more complex models to handle optionality, although the more complex models will inherit many of the interesting properties of the linear pricing model that I discuss here.

Arbitrage Free Pricing Means There Is a Clean Discount Curve

If we make two justifiable assumptions, arbitrage-free pricing implies that there is a well-defined discount curve that prices all traded instruments. The first assumption is that the set of instruments is complete, which I will simplify as it being possible to trade zero coupon bonds of any maturity. The second is that there are no transaction costs; we can always trade at the mid price.

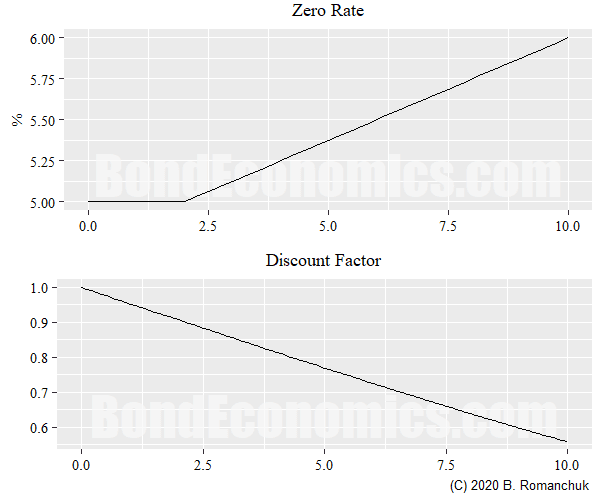
The figure above shows the discount curve and the associated zero curve (using interest rate levels that developed market participants can only fantasize about in 2020). The discount curve is the price of a zero coupon bond that matures a certain number of years in the future, the zero rate is the associated yield of the bond. (I used the mathematical quote convention, but market conventions can vary. This is why you want to work with discount curves and not zero curves whenever possible.) For example, if the price of the zero coupon of maturity T is 0.8, that means you can buy $100 face value of the bond for $80 now (and you get the $100 par value at maturity).

(Most traded bonds have coupons, and fitted curves are typically par coupon curves -- for example, the Fed H.15 release. The earlier linked primer describes this relationship.)

Although it is easy to see that we can replicate a coupon bond with a strip of zero coupon bonds (since the zeros are normally stripped payments of a coupon bond), we can replicate forwards as well. For example, take the 5-year rate, 5 years forward. All we need to do is sell short the 5-year zero, with a current market value of $100 (par value = 100/(discount price)), and buy $100 market value of the 10-year zero (face value = $100/discount price).

We have a structure with the following properties.

• Initial investment of $0.
• Required known payment to be made in 5 years (the face value of the short 5-year position).
• A known payment to be received in 10 years (the face value of the long 10-year position).

This is economically equivalent to a forward purchase of a 5-year zero coupon bond (no initial investment, but a contractual commitment to buy a bond at a future date).

Although the assumptions made might sound implausible to some, they are entirely reasonable in this context.

• If we introduce transaction costs, we just have a blurry "fair value" zone around the curve defined by mid pricing. Since we know transaction costs exist, it is perfectly fine to use the mid point, and then put a bid/offer around model fair value for traded instruments. Attempting to model a fair value range would be a waste of resources to compute and store.
• The assumption of market completeness is fine for swaps (although we can only price out to finite maturities), since we can trade a zero coupon swap for any business day. For bonds, the assumption is more awkward, since we are often working with a finite number of bonds. A fitted curve is just one out of an infinite number of curves that can match observed bond prices.

Curve Representation

If we define the yield curve with a continuous time axis, it takes an infinite amount of information to encode an arbitrary curve. (In practice, the upper bound for specification is finite, since maturities are defined by business day, so the number of points equals the umber of business days per year times the number of years in the curve.) This is too much information, and so we use a functional form to reduce the amount of information used to fit the curve.

• For spot swaps, you typically can get away with almost any functional structure. The problem is fitting short tenor forwards; if your curve generates jumpy forwards, you can end up off market. 
• Fitting bond curves is a black art, particularly for curves with only a handful of bonds. My experience is that any technique you use to "clean up" the look of the curve creates nasty side effects on the time series properties of the fitted curve. 

Curve is Invariant to Probability Distribution

An important property of the linear arbitrage pricing core is that it is invariant to the probability distribution of future rates. If we build a zero-cost arbitrage portfolio (see the technical appendix of my arbitrage primer), all future cash flows have to end up cancelled or a fixed positive amount, as the (almost) linear payoff could otherwise blow up if there is an unmatched negative cash flow.

This means that the dealer swap/swaptions market can trade off two independent pricing grids: the benchmark spot swap grid, and the volatility cube. Counterparties can argue furiously over the pricing of the implied volatility of swaption that is a fixed offset to at-the-money for hours, even while the spot swap curve is oscillating wildly. (Exchange-traded options with fixed strikes are not isolated in this fashion.)

This makes econometric analysis with yield curves feasible, since can just look at spot and forward curves, and not worry about the probability distribution around the forwards. As soon as we want to start pricing nonlinear instruments, the relationship between the pricing time axis and the real-world time axis becomes more of an issue.

Passage of Calendar Time

The invariance to the probability distribution of future interest rates helps explain one of the theoretical issues around yield curve modelling: the time axis within the model pricing is not the same thing as the passage of calendar time.

At a given time t, we can use the yield curve to price future cash flows in an internally consistent fashion, and construct arbitrage trades if we find gullible counter-parties. But we we pass to date t+1, there is no reason why the new curve must bear any relationship to the curve at time t. Nobody is willing to trade instruments at a previous day's price, so there is no mechanism to construct an arbitrage portfolio that bridges calendar time.

Efficient Markets Hypothesis to the Rescue...

The efficient markets hypothesis offers a way to bridge calendar time. We assume that expected returns for all fixed income instruments are equal. This makes sense -- if expected returns are the same, it is not easy to beat the index with duration strategies. Given the haplessness of most duration management, this does accord with observed data.

This insight allows us to apply option pricing theory to fixed income. Unfortunately, there are a large numbers of degrees of freedom to the probability distribution. Meanwhile, fixed income pricing is vexed by a problem that is not a concern for asset classes: the discount rate used for pricing is the same variable driving pricing. Other asset classes can just use a discount curve to manage this feat, with limited worries about the probability distribution of rates.

Foiled by the Term Premium

It is very easy to test whether observed interest rates are scattered around forward rates consistent with the forward rate is the mean of the distribution. And we find that this is not in fact the case. Long duration bonds tend to outperform shorter duration ones (even if we attempt to correct for the fact that most developed countries have been in a secular bond bull market).

To work around this, we can attempt to decompose observed rates into two unmeasurable components: the term premium, and an unbiased expectation for future interest rates. Although there is a large number of suggested ways to make this decomposition, each has drawbacks.

Affine Term Structure Models

We can attempt to tie together the observed yield and volatility surfaces on different days with a more sophisticated mathematical model. The most-heavily discussed class of models that do this are the affine term structure models.

Option pricing gurus that I have been in contact with absolutely adore some of these models. However, they are using them to analyze types of trading activity that I was not involved with, and so I never had any reason to delve into the models. All I can safely say is that some of these models are useful -- but affine term structure models are an extremely wide class of models.

The models that I looked at were the popular ones (typically developed by central bank researchers) that decomposed observed nominal yields (or inflation breakevens) into at least two components (unbiased expectation and a term premium), but sometimes more (liquidity premium, etc.). The models that I looked at had obvious flaws, and underperformed the simplest model (constant term premiums) in the period after model publication. (The models performed better before publication, since they would have not been published otherwise.)

In any event, these models do not offer much in the way of useful information for interest rate forecasts. I have seen attempts to do so, but this analysis was less convincing than reading candlestick charts.

Forward Time Axis Not Same As Calendar Time

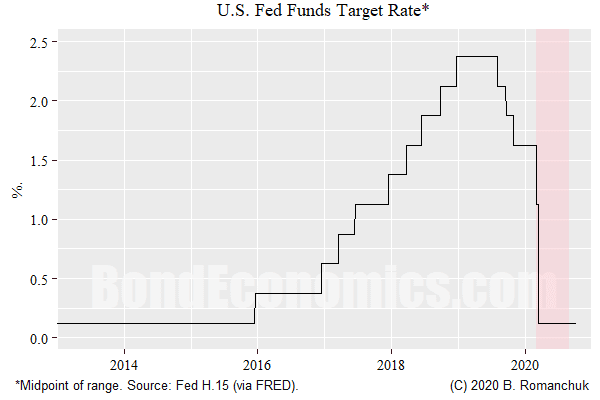
We cannot confuse the forward time axis in a model with the passage of calendar time. The plot above shows the evolution of the Fed Funds rate since 2013. It is a safe bet that we will never see a market forward curve that resembles this evolution.

Forward rates are set in a level so that they match what relative value investors believe are "reasonable." Those "reasonable" forward curves are smooth, and do not exhibit the jagged movements of time histories of realized rates. Even if we blurred the series with some noise, experienced market participants could tell at a glance whether an interest rate trajectory over a multi-year horizon is an instantaneous forward rate curve, or a realized path of short rates.

As such, we should not expect the time series of properties of interest rates to match what might be inferred from the dynamics of a arbitrage-free pricing model. Although this is not a particularly exciting insight from the context of interest rate trading -- everybody has figured this out already -- it has some awkward implications for dynamic stochastic general equilibrium modelling. (A topic that I will return to in a coming article.)

Concluding Remarks

The use of fitted curves is extremely common in macro analysis, and so some knowledge of the pricing theory for linear instruments is useful. However, the flashier part of fixed income pricing models involves option pricing. Generating the probability distribution from benchmark instrument pricing is not an easy task. 

Even for linear instruments, the term premium poses quite difficult analytical challenges for the analysis of the evolution of the market over time. It creates a wedge between arbitrage-free forwards, and the unbiased expectation for the path of interest rates. It also ensures that there is a gap between calendar time and forward axis time.